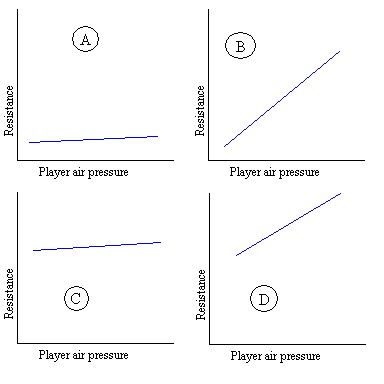
In each graph the horizontal axis represents the amount of air pressure applied to the instrument by the player, the vertical axis represents the amount of back-pressure or resistance the player feels coming from the instrument. The resulting sound volume and the volume of air required are not in these graphs. These graphs probably represent extremes.

The way I see things, the starting point of the graph (vertically) is determined by the bore size: large bore = low initial resistance, small bore = high(er) initial resistance. The slope of the graph is linked to the taper of the bore. An instrument with very little taper (cylindrical) will have a rising graph, an instrument with a high degree of taper (conical) will have a flat graph.

 

Graph "A" shows a large bore, conical instrument: the resistance starts out low due to the large bore, and doesn't increase very much as the air pressure applied by the player increases due to the large taper of the bore. Such an instrument would feel extremely open or "free blowing". Graph "B" shows the same large bore instrument with a cylindrical bore. Because this instrument has little taper resistance increases rapidly as player air pressure increases. Such an instrument would start out feeling "open" but soon feel "tight" as the player increases the air pressure. Graph "C" shows a small bore, conical instrument; initial resistance is higher than it is on the large bore instrument, but doesn't increase very much because of the large taper. An instrument with these qualities would feel quite free blowing in spite of having a small bore. Finally graph "D" shows a small bore, cylindrical instrument: high initial resistance that increases further with more air pressure. Of course it might well be that these graphs in fact could be curves with resistance being similar to graph A or C at first and as player air pressure is increased suddenly rising considerably, more like graph B or D. That would be similar to "hitting a wall".

 

The relation to volume of air required

The less resistance there is, the easier it is to blow a larger volume of air into the instrument. The graphs above don't give the volume of air required for each bore "strategy". However, this can be inferred from the above graphs. For example, graph A requires quite a bit of air at low sound volumes and since there is little resistance the volume of air required goes up rapidly. If in the above graphs you substiture "Volume of air required" for "Resistance" and "Volume of sound" for "Player air pressure", the graphs are crossed diagonally. In other words, the resistance and air pressure of graph A would correspond to the volume of air and sound of graph D and vice versa. Likewise, graphs B and C correspond to each other.

 

The relation to sound volume

Given for the moment that bell size is equal, to produce a specific low sound volume a small bore instrument should require less volume of air than a large bore instrument, but the player will need to overcome more resistance than on a large bore instrument. As the desired volume level increases, an instrument which is more conical will have less resistance to overcome, requiring less increase in air pressure in addition to the increase in volume of air than an instrument which is more cylindrical. The size of the bell is another variable in this equation. It serves as an amplifier: the larger the bell, the more volume will be produced for the same amount of effort.

 

Examples of instruments

Might it be possible to name some instruments to go with the graphs above? My attempt at that would be something along the following lines, and please do correct me if I am wrong or if you have a better example to illustrate things.
Graph A, large bore, high taper: Flip Oakes' Wild Thing.
Graph B, large bore, low taper: Holton, from what I am told.
Graph C, small bore, high taper: Conn 38B Connstellation. The 38B probably is the classic example of "graph C" (at least in terms of this website.... ).
Graph D, small bore, low taper: Any suggestions?

Naturally there is quite a bit of room between these extremes. Most #1 (0.438") bore Conn's would probably come in somewhere between "C" and "D". With the current trend towards large(r) bore instruments, I suspect most modern instruments are somewhere between graphs "A" and "B".

A good example of the difference between a large bell and a small bell is the difference in feel between the Conn 36B Lightweight Connstellation and the Conn 38B Connstellation. The two instruments are essentially identical (at least for purposes of this article), except the 36B has a 4 5/8" bell while the 38B has a large 5 1/8" bell. Eventhough the internal bore and taper of the 36B and 38B are the same, the 36B will require more effort to produce the same volume of sound as the 38B since it has a smaller bell. Conn in its 1966 catalog describes the 38B as a "large bore feel" and the 36B as a "medium bore feel". And the size of the bell is the only difference.

 

Player preferences

Different people of course prefer different instruments and different "feels". Some people like to blow "through" and instrument, others prefer to have something to blow "against". The "through" people will probably dislike small(er) bores and higer resistance instruments, in stead gravitating towards an instrument that behaves like graph "A", above. They might feel like they can't get rid of their air in an instrument with a smaller bore and more resistance. The "against" people on the other hand would probably dislike the "graph A" instrument on account that it swallows them up. They might feel like they are expending their air in an instant, there is "no resistance". These people might prefer something "open" and "free blowing" at lower sound levels (and air volume), but not like the large volume of air required in a large bore instrument with a lot of taper such as graph A. They might prefer something like graph B which is more "closed". Or, perhaps something like graph C, which generally requires less volume (more closed), but which doesn't have the large increase in resistance. To each his or her own.

The other day I receiverd a very interesting e-mail from Richard Gosnay, commenting on the article I wrote called The "feel" of a bore. In that e-mail he offered a different perspective on the subject at hand. The relevant part of his e-mail is copied below.

The comments about the feel of a bore [in the article The"feel" of a bore] are very consistent with terms used by brass musicians and teachers. However, they do not follow laws of physics. I think that a more practical and scientific approach to brass playing is more instructive to us all. Resistance is a very, very over-used term in brass playing. Whenever I hear a person say that an axe has a lot of resistance, I hold it with my mouth completely around the mouthpiece. Then I huff as hard as I can into it. Almost without variation, my huff finds no resistance. And this, of course is far more air than we use to actually play a note. An instrument with resistence would be tight in the low register because that is a large volume of air. But brass players think they find resistance in the high register. When we feel like a brass instrument is resisting our airstream, it is because we are not playing in tune. This could be due to our limitation in technique. More likely, it is due to intrinsic limitations to the instrument (which is why some instruments seem open and some tight to the same player). Instruments also have dead notes if they have solders that unfortunately deaden the bell precisely at locations of nodes for particular wavelength!

Bernouli, or Birnouli, or whatever that physicist's name was, developed principles regarding matter (i.e. our airstream) passing through fixed volumes. With respect to resistance, the bore or any instrument has no effect. This is because the throat of the mouthpiece is smaller than the bore. Any airstream passing through the mouthpiece is not going to resist passing into the bore. As the air passes through the throat, the pressure immediately drops. And remember, when we are playing high notes, the aperture between our lips is even smaller than the mouthpiece throat! Whether the bore is cylindrical or conical has no bearing on resistance (as long as it does not shrink smaller than the size of the mouthpice throat).

When we have instruments that play tight, or we must force air into with great force, the answer is NOT to address resistance to the airstream. The answer is to address the limitations of the physical and acoustical properties of the instrument. This could mean adjusting the wavelengths so that they fit the frequency (i.e. playing in tune). A valved instrument may need a section of tubing slightly cut. Braces on the bell section might need to be moved or removed. Sometimes, we just need to simply use alternate fingerings or slide positions to more accurately form the optimal wavelength. Many mouthpieces, these days are hopelessly inappropriate to the instrument's acoustical properties. I have an anecdote of my own:

When I was in music school, one of my best talents was versatility. I studied tenor trombone. But I was the orchestra's substitute bass trombonist too. And I played any euphonium parts that were needed. So, when I was impressed by the sound of some European orchestras, I became interested in playing alto trombone. I found a used Yamaha at a good price, and I was on my way. When I would practice, I became convinced that I had bought a lemon. The thing was hopelessly out of tune all the time. I couldn't keep any position consistent. Instead of having a trombone with 7 positions, I had an alto with about 100 different positions. Then, I tried something that had amazing results. I heaved all the small Bach mouthpieces that I felt comfortable with because of my tenor playing. I picked up the Yamaha mouthpiece that came with the instrument. Immediately, all the positions fell into place. The instrument became as loud and resonant as I wanted. I might add that the mouthpiece is a real pea-shooter. And, of course, the bore of the alto is small. But they have absolutely no resistance.

I learned that all instruments have mouthpieces that fit into the wavelengths created by the column such that they easily produce desired frequencies. And it is futile to fight these conditions. I no longer try to shoe-horn mouthpieces with which I am comfortable into instruments. My bass has a bigger mouthpiece than I like. My alto has a smaller one. But they sound much more resonant, and play better in tune, and give less of a feeling of resistance than they would if I used other mouthpieces. I adapt to the physics, because the physics will not adapt for me.

Music is made of sound. And the things that we change are time, frequency, and amplitude. If we simplify our understanding to these ideas, it is much easier to play our instruments. When teachers exhort us to fill the horn, they are not helping. The richness of tone is not a matter of filling the horn (which can't be filled because it has a big hole in the end). We need to think of increasing air volume only to increase amplitude of the sound waves (loudness=amplitude). We do not use more air to make the tones sound better. That is done by buzzing frequencies with our lips that are acoustically supported by the length of tubes that form our instruments because they match the wavelengths of the frequencies.

My alto is not any easier to play than my tenor for any particular high note. If I play well, it just sounds better. This is because the instrument is pitched higher. So, any given note, say a high E flat, is lower in the overtone series on the alto than on the tenor. It rings more overtones, so it sounds nicer. That's all there is to it. The same E flat on my tenor is just as easiy to produce. It just sounds thinner and wimpier. And there is nothing I can do about it because of physics.

Richard Gosnay

 

Thanks to Christine Derksen and Richard Gosnay of the "Conn Loyalist." The site is: http://www.xs4all.nl/~cderksen/index.html